asdf11111111111111111111

https://www.acmicpc.net/problem/16917

2초 / 512MB

문제

현진 치킨에서 판매하는 치킨은 양념 치킨, 후라이드 치킨, 반반 치킨으로 총 세 종류이다. 반반 치킨은 절반은 양념 치킨, 절반은 후라이드 치킨으로 이루어져있다. 양념 치킨 한 마리의 가격은 A원, 후라이드 치킨 한 마리의 가격은 B원, 반반 치킨 한 마리의 가격은 C원이다.

상도는 오늘 파티를 위해 양념 치킨 최소 X마리, 후라이드 치킨 최소 Y마리를 구매하려고 한다. 반반 치킨을 두 마리 구입해 양념 치킨 하나와 후라이드 치킨 하나를 만드는 방법도 가능하다. 상도가 치킨을 구매하는 금액의 최솟값을 구해보자.

입력

첫째 줄에 다섯 정수 A, B, C, X, Y가 주어진다.

출력

양념 치킨 최소 X마리, 후라이드 치킨 최소 Y마리를 구매하는 비용의 최솟값을 출력한다.

제한

• 1 ≤ A, B, C ≤ 5,000
• 1 ≤ X, Y ≤ 100,000

• 반반 치킨을 두 마리 구입해 양념 치킨 하나와 후라이드 치킨 하나를 만드는 방법도 가능
• 양념 치킨 한 마리의 가격은 A원, 후라이드 치킨 한 마리의 가격은 B원, 반반 치킨 한 마리의 가격은 C원
• 다섯 정수 A, B, C, X, Y
• 1 ≤ A, B, C ≤ 5,000
• 1 ≤ X, Y ≤ 100,000
• 양념 치킨 최소 X마리, 후라이드 치킨 최소 Y마리를 구매하는 비용의 최솟값

풀이 (C++)

• iostream
• algorithm
• 브루트 포스

풀이 과정

문제의 핵심은 반반치킨

반반치킨은 두 개 단위로 구매할 수 있고, 반반치킨 두 개 = 양념치킨 하나 + 후라이드치킨 하나

치킨을 딱 맞게 구매할 필요 없이 최소 X마리, Y마리 구매하면 되므로 가격만 싸다면 개수가 넘어도 된다

반반치킨의 개수를 0개부터 시작하여 X, Y 중 더 큰 값까지 살펴본다

최악의 경우가 100000 ( 0이 5개 )이므로 충분히 2초 내에 가능 ( 브루트 포스의 근거 )

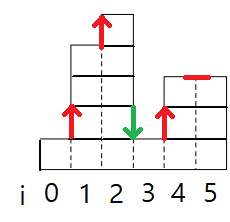
다음은 x=3이고 y=2일 때 오로지 개수만 따진 표이다

다음과 같은 4가지 경우의 수가 나오며, 모든 경우의 수에 대해 최소 가격을 찾아주면 된다

제일 오른쪽 줄은 반반치킨으로 만든 양념/후라이드의 갯수를 칭한다

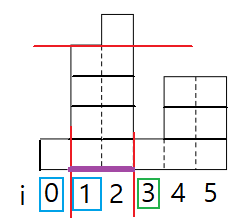
초록색 네모와 같이 음수가 나올 수 있다 ( 사야 할 개수가 음수라는 뜻이므로 1개가 남는다는 뜻 )

그러나 위에서 살펴봤듯 치킨은 남을 수 있으니 가격을 계산할 때는 음수는 0으로 취급한다

남을 수 있다고 해서 x, y보다 더 사는 경우는 무조건 최솟값보다 더 사게 되므로 x, y 중 큰 수까지만 고려해준다

( 목표는 몇 개를 사던지 간에 최소 x, y 개를 사기만 하면 되는데, 그 중 최소 가격을 찾는 것이기 때문 )

1. 7번 줄 // 수 입력 순서 주의
2. 9번 줄 // 어짜피 반반치킨은 두 개 단위로 구매해야 하므로 값을 두배시켜 준다
3. 10~17번 줄 // ban은 반반치킨의 갯수( 의 1/2개 ) , x, y중 더 큰 값까지 살펴본다
   1. 11~12번 줄 // 양념 후라이드 단일 구매 갯수에서 반반치킨에 의해 감소되는 양 계산
   2. 13~14번 줄 // 만약 음수라면 ( 그만큼의 치킨이 남는다면 ) 0으로 처리
   3. 15번 줄 // 가격 계산
   4. 16번 줄 // 정답 비교, 초기화를 -1로 해두어서 대소비교가 적절히 이루어지도록 한다 ( 0으로 해두면 0이 계속 최솟값일 것이므로, 그런데 a,b,c 모두 최솟값이 1이라 가격이 0인 경우는 없긴 하다 )
4. 18번 줄 // 정답 출력

주의사항

1. 정답이 int 범위를 넘을 수 있다 ( 곱하기 형변환 주의 / int 끼리 곱한다고 long long 안된다==> 이 코드에서는 변수부터 long long으로 선언해서 해결 )
2. 주어진 치킨의 개수는 '최소'임 ( 치킨이 남을 수 있음 )
3. 정답 비교할 때 가능한 경우의 최솟값보다 작은 수 또는 최대값 보다 큰 수로 초기화 해둬야 한다

https://www.acmicpc.net/problem/16968

1초 / 512MB

문제

상도시의 차량 번호판 형식이 주어졌을 때, 가능한 차량 번호판의 개수를 구해보자.

• 번호판에 사용할 수 있는 숫자는 0, 1, 2, ..., 8, 9이다.
• 사용할 수 있는 문자는 a, b, c, d, ..., y, z이다.
• 차량 번호판의 형식은 최대 4글자이고, c와 d로 이루어진 문자열로 나타낼 수 있다.
• c는 문자가 위치하는 자리, d는 숫자가 위치하는 자리이다.
• 같은 문자 또는 숫자가 연속해서 2번 나타나면 안 된다.

예를 들어, 형식이 "cd"이면, a1, d4, h5, k4 등이 가능하다. 형식이 "dd"인 경우에 01, 10, 34, 69는 가능하지만, 00, 11, 55, 66은 같은 숫자가 2번 연속해서 불가능하다.

입력

첫째 줄에 차량 번호판의 형식이 주어진다. 형식은 길이가 4보다 작거나 같으며, c와 d로만 이루어져 있다.

출력

첫째 줄에 가능한 차량 번호판의 개수를 출력한다.

• 0, 1, 2, ..., 8, 9
• a, b, c, d, ..., y, z
• 최대 4글자
• c는 문자가 위치하는 자리, d는 숫자가 위치하는 자리
• 같은 문자 또는 숫자가 연속해서 2번 나타나면 안 된다
• 가능한 차량 번호판의 개수

풀이 (C++)

• iostream
• string

풀이 과정

연속으로만 나오면 안 된다 그리고 경우의 수만 구하면 된다

처음 가능한 '숫자'의 경우의 수는 10, 이후 반복 출현할 경우 9 // ex) dddd => 10*9*9*9

처음 가능한 '글자'의 경우의 수는 26, 이후 반복 출현할 경우 25 // ex) cccc => 26*25*25*25

따라서 '숫자'일 경우에는 '글자'의 경우의 수를 26으로 복구해줘야하고

'글자'의 경우에는 '숫자'의 경우의 수를 10으로 복구해줘야 한다

( 같은 종류가 연속되는 경우가 아니므로 )

ex) cdcd => 26*10*26*10

1. 8번 줄 // 입력 받음
2. 11번 줄 // 정답은 1로 준비 ( 최대 경우의 수 26*25*25*25가 int 범위 내이므로 int로도 가능 )
3. 13~22번 줄 // 한 글자씩 확인한다
   1. 13~17번 줄 // 만약 d일 경우
   2. 정답에 가능한 숫자 경우의 수 곱함
   3. c는 26으로 초기화
   4. 수가 연속될 것에 대비해 num는 9로
   1. 18~22번 줄 // 만약 d일 경우
   2. 정답에 가능한 숫자 경우의 수 곱함
   3. 수가 연속될 것에 대비해 num는 25로
   4. num는 10으로 초기화
4. 24번 줄 // 정답 출력

주의사항

1. 처음 ans를 0이 아닌 1로 둬서 경우의 수를 계속 곱해준다

https://www.acmicpc.net/problem/1725

https://www.acmicpc.net/problem/6549

1725: 2초 / 128MB

6549: 1초 / 256MB

문제 (6549)

히스토그램은 직사각형 여러 개가 아래쪽으로 정렬되어 있는 도형이다. 각 직사각형은 같은 너비를 가지고 있지만, 높이는 서로 다를 수도 있다. 예를 들어, 왼쪽 그림은 높이가 2, 1, 4, 5, 1, 3, 3이고 너비가 1인 직사각형으로 이루어진 히스토그램이다.

히스토그램에서 가장 넓이가 큰 직사각형을 구하는 프로그램을 작성하시오.

입력

입력은 테스트 케이스 여러 개로 이루어져 있다. 각 테스트 케이스는 한 줄로 이루어져 있고, 직사각형의 수 n이 가장 처음으로 주어진다. (1 ≤ n ≤ 100,000) 그 다음 n개의 정수 h1, ..., hn (0 ≤ hi ≤ 1,000,000,000)가 주어진다. 이 숫자들은 히스토그램에 있는 직사각형의 높이이며, 왼쪽부터 오른쪽까지 순서대로 주어진다. 모든 직사각형의 너비는 1이고, 입력의 마지막 줄에는 0이 하나 주어진다.

출력

각 테스트 케이스에 대해서, 히스토그램에서 가장 넓이가 큰 직사각형의 넓이를 출력한다.

• 가장 넓이가 큰 직사각형
• 1 ≤ n ≤ 100,000
• 0 ≤ h ≤ 1,000,000,000
• 직사각형의 너비는 1

풀이 (C++)

• cstdio
• vector
• stack

풀이 과정

1725와 6549는 출처가 완전히 같은 쌍둥이 문제

1725는 6549에서 반복문만 제거해주면 되므로 6549를 보자

높이 제한이 1000000000 (0이 9개)이고, N이 100000까지 가능하므로 높이를 기준으로 뭔가 하려는 순간 바로 시간 초과

고로 가로를 중심으로 보되 어떤 변화가 있는 부분( 높이의 대소관계가 변화는 지점 )을 중점적으로 본다

다음과 같은 입력이 있다고 가정하자

6 1 4 5 1 3 3

기본적으로 입력받은 순으로 스택에 넣는다

그 과정에서 일어날 수 있는 상황은 다음 두 가지밖에 없다

1. 넣으려는 수가 이전 수보다 크거나 같다 (빨간 화살표) => 스택에 push
2. 넣으려는 수가 이전 수보다 작다 (초록 화살표) => 스택에 있는 수들 중 넣으려는 수보다 큰 수들이 있는지 확인해준 후 push

특히 2번 경우를 잘 해결하는 것이 이 문제를 해결하는 것과 같다고 할 수 있다

이 상황이 언제 일어나는지 잘 기억해두자 ( 이하 '초록 화살표, 확인 상황'으로 통칭 )

확인하는 법

상황) 현재 i가 3이라서 i가 2일때 높이 (5)보다 높이 (1)이 작아서 확인하게 된 경우

스택에 들어있는 숫자들은 하늘색, 지금 기준이 되는 숫자는 초록색이라고 하자

1. i=2 일 때 만들 수 있는 최대 직사각형 = i=2일 때 높이 (5) x 너비 (3-1-1=1) = 5 (노란색)
2. i=1 일 때 만들 수 있는 최대 직사각형 = i=1일 때 높이 (4) x 너비 (3-1-0=2) = 8 (남색)
3. i=0 일 때 높이 = i=3일 때 높이이므로 확인 종료

이 과정에서 너비를 구하는 방법이 핵심이다

상황) 현재 i가 3이라서 i가 2일때 높이 (5)보다 높이 (1)이 작아서 확인하게 된 경우, 2는 이미 넓이 5로 확인 후 pop되었고, 다음 수인 1을 확인하려고 한다

1일 때 높이 4의 입장에서 보면 왼쪽에 0은 스택에 있고 오른쪽에 2는 스택에 없다

그리고 2는 현재 i인 3보다 작으므로, 높이 4보다 같거나 클 것임이 보장되어있다 ( 2의 높이가 만약 1의 높이보다 작았다면 이미 i = 2일 때 확인과정을 거쳐 스택에서 pop되었을 것이기 때문 )

따라서 높이는 4이고 너비는 좌우로 가능한 만큼 최대로 뻗어나갔을 때의 길이가 된다 (보라색선)

이때 가장 오른쪽은 현재 i 보다 1 작은 수일 것이고, 가장 왼쪽은 다음 stack에 맨 위에 있는 수+1일 것이다

$$ stack.top()+1 \leq x \leq i-1 $$

따라서 길이는 i-1-stack.top()

$$(i-1)-(s.top()+1)+1 = i-1-stack.top()$$

그런데 왼쪽에 더 이상 스택에 들어있는 수가 없을 수도 있다 이럴 경우에는 가장 왼쪽이 0이 되므로

$$ 0 \leq x \leq i-1 $$

따라서 길이는 i

1. 9, 12번 줄 // 0을 받기 전까지 무한 반복 구현
2. 14~16번 줄 // 수 입력받기
3. 18번 줄 // 정답 받아줄 변수 선언 ( 0으로 초기화, long long )
4. 19~28번 줄 // for문으로 가로를 기준으로 하나씩 확인
5. 20~26번 줄 // 이번 문제의 핵심! 
   1. 20번 줄 // while이 돌아가는 기준 잘 확인 ( 스택이 비어있지 않고 위의 "초록 화살표"일 경우 )
   2.  21~22번 줄 // 높이만 저장 후 스택에서 pop ( 이 시점부터 스택의 맨 위 stack.top()은 방금 뽑아낸 높이의 왼쪽에 있는 수 )
   3.  23~24번 줄 // 너비를 구해준다 ( 스택이 비었을 경우 i 아니면 i-1-stack.top() )
   4. 25번 줄 // 너비 * 높이로 넓이 구한 후 정답 변수 갱신 ( 이 때 형 변환 주의 !! )
6. 27번 줄 // 왼쪽에 있으면서 현재 높이보다 큰 경우를 모두 확인했으므로 push
7. 29~35번 줄 // 적절한 초록색 화살표를 만나지 못해 스택에 수가 남아있는 경우가 있다 이럴 경우에는 너비의 오른쪽 끝을 현재 i가 아닌 n으로 잡고 똑같은 while문을 돌려줌으로써 스택을 비워준다 ( 모든 경우의 수를 다 비교해본다 ) ( 제일 끝을 높이 -1의 임의의 초록색 화살표로 만들어 줬다고 생각하면 된다 )

주의사항

1. 넓이는 int범위를 넘을 수 있다
2. int와 int를 곱하면 long long이 되지 않는다. 곱하기 전에 형변환을 해 줘야 한다 ( 풀이에는 처음부터 높이를 long long으로 변환해둠으로써 처리 )
3. 정답 변수를 처음에 0으로 초기화해둬서 비교가 적절히 이루어지도록 한다
4. 1725에 제출할 때에는 반복문을 제거하자

https://www.acmicpc.net/problem/4948

2초 / 512MB

문제

이 문제는 아주 평범한 배낭에 관한 문제이다.

한 달 후면 국가의 부름을 받게 되는 준서는 여행을 가려고 한다. 세상과의 단절을 슬퍼하며 최대한 즐기기 위한 여행이기 때문에, 가지고 다닐 배낭 또한 최대한 가치 있게 싸려고 한다.

준서가 여행에 필요하다고 생각하는 N개의 물건이 있다. 각 물건은 무게 W와 가치 V를 가지는데, 해당 물건을 배낭에 넣어서 가면 준서가 V만큼 즐길 수 있다. 아직 행군을 해본 적이 없는 준서는 최대 K무게까지의 배낭만 들고 다닐 수 있다. 준서가 최대한 즐거운 여행을 하기 위해 배낭에 넣을 수 있는 물건들의 가치의 최댓값을 알려주자.

입력

첫 줄에 물품의 수 N(1 ≤ N ≤ 100)과 준서가 버틸 수 있는 무게 K(1 ≤ K ≤ 100,000)가 주어진다. 두 번째 줄부터 N개의 줄에 거쳐 각 물건의 무게 W(1 ≤ W ≤ 100,000)와 해당 물건의 가치 V(0 ≤ V ≤ 1,000)가 주어진다.

입력으로 주어지는 모든 수는 정수이다.

출력

한 줄에 배낭에 넣을 수 있는 물건들의 가치합의 최댓값을 출력한다.

• N개의 물건 N(1 ≤ N ≤ 100)
• 무게 W W(1 ≤ W ≤ 100,000)
• 가치 V V(0 ≤ V ≤ 1,000)
• 최대 K무게 K(1 ≤ K ≤ 100,000)
• 배낭에 넣을 수 있는 물건들의 가치의 최댓값

풀이 (C++)

• iostream
• vector
• algorithm
• 동적 계획법

풀이 해설

동적 계획법으로 풀 수 있다

다음과 같이 구현할 수 있다 

예제 입력 1
4 7
6 13
4 8
3 6
5 12

3 7 
3 8 
1 5 
2 7

입력 받은 순서대로 살펴본다

1000000000(0이 9개)면 1초인데 대략 계산해보면

N*K = 10000000 (0 7개)이므로 충분히 2초 내에 작동함

1. 17~19번 줄 // 앞까지 도착한 숫자들은 전부 각 무게에서 여태껏 최대의 가치들이므로 이번 무게로 이행시켜준다 (빨간색 화살표)
2. 20번 줄 // 현재 물건의 무게가 최대 무게 이내일 경우 해당 무게의 칸에 이미 있는 값과 비교하여 큰 것을 넣어준다 (초록색 화살표)
3. 21~25번 줄 // 이전 숫자들을 보면서 이번 무게와 합쳤을 때 최대 무게를 넘지 않는 경우에는 해당하는 무게의 칸에 이미 있는 값과 비교하여 큰 것을 넣어준다 (파란색 화살표)
4. 28~30번 줄 // 맨 마지막 물건을 한번 돌면서 정답을 찾아낸다

주의사항

1. 저장하려는 위치에 이미 수가 있을 수도 있으니 꼭 비교해서 더 큰 수만 저장하도록 해야 한다
2. dp는 0으로 초기화 해준다 (풀이 해설 2번에서 비교할 때 없는 경우를 0으로 비교해야 하므로)
3. dp[i-1]과 같은 경우 segmentation fault (dp[-1] 참조) 발생할 수도 있으니 꼭 맨 앞 배열 한 칸은 비워둔다
4. dp 배열이 커서 segmentation fault가 날 수도 있다 -> 전역 범위로 (main 밖) 빼준다 // BOJ에서는 통과했다

https://www.acmicpc.net/problem/3053

1초 / 128MB <스페셜 저지>

문제

19세기 독일 수학자 헤르만 민코프스키는 비유클리드 기하학 중 택시 기하학을 고안했다.

택시 기하학에서 두 점 T1(x1,y1), T2(x2,y2) 사이의 거리는 다음과 같이 구할 수 있다.

D(T1,T2) = |x1-x2| + |y1-y2|

두 점 사이의 거리를 제외한 나머지 정의는 유클리드 기하학에서의 정의와 같다.

따라서 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.

원: 평면 상의 어떤 점에서 거리가 일정한 점들의 집합

반지름 R이 주어졌을 때, 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램을 작성하시오.

입력

첫째 줄에 반지름 R이 주어진다. R은 10,000보다 작거나 같은 자연수이다.

출력

첫째 줄에는 유클리드 기하학에서 반지름이 R인 원의 넓이를, 둘째 줄에는 택시 기하학에서 반지름이 R인 원의 넓이를 출력한다. 정답과의 오차는 0.0001까지 허용한다.

1. D(T1,T2) = |x1-x2| + |y1-y2|
2. 택시 기하학에서 원의 정의는 유클리드 기하학에서 원의 정의와 같다.
3. 유클리드 기하학에서 원의 넓이와, 택시 기하학에서 원의 넓이를 구하는 프로그램
4. R은 10,000보다 작거나 같은 자연수
5. 정답과의 오차는 0.0001까지 허용

풀이 (C++)

• iostream
• cmath

풀이 과정

택시 기하학에서 D(T1,T2) = |x1-x2| + |y1-y2|인데 x1과 y1을 원점 (0,0)으로 고정하면 r=|x2|+|y2|이므로 원은 그림과 같이 마름모 형태이다.

이때 마름모의 넓이는 $$2r^2$$

유클리드 기하학에서 원의 넓이는 $$\pi r^2$$

1. 1~3번 줄 // #define _USE_MATH_DEFINES을 #include <cmath> 전에 적어줌으로써 cmath의 M_PI (원주율)을 쓸 수 있도록 한다
2. 9~10번 줄 // cout << fixed와 cout.precision()을 이용하여 소수점 6자리로 고정 및 반올림한다 (cplusplus.com 참고)
3. 11~12번 줄 // 답을 출력한다

주의사항

1. 스페셜 저지 문제이므로 마름모의 넓이는 정수 그대로 출력해도 (예시처럼 소수점 6자리까지 0을 표기하지 않아도) 된다.
2. 적절한 정도의 정확성을 가진 원주율을 사용하자
3. 개행 명심

https://www.acmicpc.net/problem/1002

2초 / 256MB

문제

조규현과 백승환은 터렛에 근무하는 직원이다. 하지만 워낙 존재감이 없어서 인구수는 차지하지 않는다. 다음은 조규현과 백승환의 사진이다.

이석원은 조규현과 백승환에게 상대편 마린(류재명)의 위치를 계산하라는 명령을 내렸다. 조규현과 백승환은 각각 자신의 터렛 위치에서 현재 적까지의 거리를 계산했다.

조규현의 좌표 (x1, y1)와 백승환의 좌표 (x2, y2)가 주어지고, 조규현이 계산한 류재명과의 거리 r1과 백승환이 계산한 류재명과의 거리 r2가 주어졌을 때, 류재명이 있을 수 있는 좌표의 수를 출력하는 프로그램을 작성하시오.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 다음과 같이 이루어져 있다.

한 줄에 x1, y1, r1, x2, y2, r2가 주어진다. x1, y1, x2, y2는 -10,000보다 크거나 같고, 10,000보다 작거나 같은 정수이고, r1, r2는 10,000보다 작거나 같은 자연수이다.

출력

각 테스트 케이스마다 류재명이 있을 수 있는 위치의 수를 출력한다. 만약 류재명이 있을 수 있는 위치의 개수가 무한대일 경우에는 -1을 출력한다.

• 좌표의 수
• x1, y1, r1, x2, y2, r2 (입력 순서)
• 위치의 개수가 무한대일 경우에는 -1을 출력

풀이 (C++)

• iostream

풀이 과정

입력 자체도 x, y, r인 것이 중심과 반지름을 뜻하는 것 같고 원의 정의 ( 한 점을 기준으로 같은 거리만큼 떨어진 점들의 집합 )와 문제의 핵심이 같으므로 두 원 사이의 관계/교점으로 풀어줍니다

1. 바깥에서 만나지 않음 : 0
2. 원 안에서 만나지 않음 : 0
3. 외접 : 1
4. 내접 : 1
5. 두 원이 일치 : -1
6. 이외 상황들 : 2

1. 4~6번 줄 // circle 자료구조를 만들어 x, y, r 입력받음
2. 14~16번 줄 // 두 원의 중심사이의 거리 (dist)와 반지름의 합 (sumr), 차 (diffr)을 제곱 상태로 구해줍니다
3. 18~25번 줄 // 이번 문제의 하이라이트, 위의 모든 상황을 잘 반영해주도록 합니다
4. 26번 줄 // 답 출력 이후 개행

제가 구현한 논리 흐름은 다음과 같습니다.

1. 중심 사이의 거리 > 반지름의 합 ==> (1) 바깥에서 만나지 않음 : 0
2. 중심 사이의 거리 == 반지름의 합 ==> (3) 외접 : 1
3. 중심 사이의 거리 < 반지름의 합 //
   1. 중심 사이의 거리 > 반지름의 차 ==> (6) 이외 상황들 : 2
   2. 중심 사이의 거리 < 반지름의 차 ==> (2) 원 안에서 만나지 않음 : 0

   3. 중심 사이의 거리 == 반지름의 차 //

      1. 중심 사이의 거리 == 0 ==> (5) 두 원이 일치 : -1
      2. 중심 사이의 거리 != 0 ==> (4) 내접 : 1

주의사항

1. 소숫점 연산은 오차가 나므로 되도록이면 피해줍니다 ( long long으로 제곱 수끼리 비교 )
2. 개행 ('\n') 잊지 않기
3. 상황 빼먹지 말고 다 구현하기
4. 입력 순서 주의

https://www.acmicpc.net/problem/9020

2초 / 256MB

문제

1보다 큰 자연수 중에서  1과 자기 자신을 제외한 약수가 없는 자연수를 소수라고 한다. 예를 들어, 5는 1과 5를 제외한 약수가 없기 때문에 소수이다. 하지만, 6은 6 = 2 × 3 이기 때문에 소수가 아니다.

골드바흐의 추측은 유명한 정수론의 미해결 문제로, 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다는 것이다. 이러한 수를 골드바흐 수라고 한다. 또, 짝수를 두 소수의 합으로 나타내는 표현을 그 수의 골드바흐 파티션이라고 한다. 예를 들면, 4 = 2 + 2, 6 = 3 + 3, 8 = 3 + 5, 10 = 5 + 5, 12 = 5 + 7, 14 = 3 + 11, 14 = 7 + 7이다. 10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재한다.

2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력하는 프로그램을 작성하시오. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력한다.

입력

첫째 줄에 테스트 케이스의 개수 T가 주어진다. 각 테스트 케이스는 한 줄로 이루어져 있고 짝수 n이 주어진다. (4 ≤ n ≤ 10,000)

출력

각 테스트 케이스에 대해서 주어진 n의 골드바흐 파티션을 출력한다. 출력하는 소수는 작은 것부터 먼저 출력하며, 공백으로 구분한다.

• 2보다 큰 모든 짝수는 두 소수의 합으로 나타낼 수 있다
• 2보다 큰 짝수 n이 주어졌을 때, n의 골드바흐 파티션을 출력
• 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력
• 4 ≤ n ≤ 10,000
• 출력하는 소수는 작은 것부터 먼저 출력
• 공백으로 구분

풀이 (C++)

• iostream
• 에라토스테네스의 체

풀이 과정

1. 6~17번 줄 // 에라토스테네스의 체 이용 (n=10000일 때 2+9998까지 확인할 수 있으므로 10000까지 확인)
2. 19~21번 줄 // 테스트 케이스의 수 T입력 받은 후 반복
3. 24~25번 줄 // left와 right을 구분하여 left는 항상 right보다 작은 수 ( 8=3+5에서 3이 left, 5가 right 출력하는 소수는 작은 것부터 먼저 출력해야 하기 때문 )
4. 24~25번 줄 //left와 right의 시작점은 n/2로 한다( 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력해야 함 // n은 항상 짝수 )
5. 26번 줄 // while(1)로 해도 가능 ( 근거는 문제에서 "10000보다 작거나 같은 모든 짝수 n에 대한 골드바흐 파티션은 존재"라고 했기 때문 )
6. 27번 줄 // left right 둘 다 소수일 경우 답을 찾은 경우 break
7. 31번 줄 // 정답 출력

주의사항

1. 만약 가능한 n의 골드바흐 파티션이 여러 가지인 경우에는 두 소수의 차이가 가장 작은 것을 출력
2. 출력하는 소수는 작은 것부터 먼저 출력 공백으로 구분
3. 4 ≤ n ≤ 10,000

https://www.acmicpc.net/problem/4948

풀이 (C++)

• iostream
• 에라토스테네스의 체